
Zadanie 1
Matematyka PP 2023 (0-1 pkt.)
Na osi liczbowej zaznaczono sumę przedziałów.

Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiór zaznaczony na osi jest zbiorem wszystkich rozwiązań nierówności
A. $|x-3,5|\geq1,5 $
B. $|x-1,5|\geq3,5 $
C. $|x-3,5|\leq1,5 $
D. $|x-1,5|\leq3,5 $
Zadanie 2
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba $\sqrt[3]{-\frac{27}{16}}\cdot \sqrt[3]{2}$ jest równa
A. $(-\frac{3}{2})$
B. $\frac{3}{2}$
C. $\frac{2}{3}$
D. $(-\frac{2}{3})$
Zadanie 3
Matematyka PP 2023 (0-2 pkt.)
Wykaż, że dla każdej liczby naturalnej $n\geq1$ liczba $(2n+1)^{2}-1$ jest podzielna przez 8.
[katex]4n(n+1)[/katex]
Liczba 8, to [katex]4\cdot 2[/katex], natomiast któraś z liczb: [katex]n[/katex] lub [katex]n+1[/katex] na pewno jest liczbą parzystą, więc ma w sobie mnożenie przez 2, dlatego można uznać, że powyższe wyrażenie dzieli się przez 8.
Rozwiązanie wideo:
Zadanie 4
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba $\log_{9}27 + \log_{9}3$ jest równa
A. 81
B. 9
C. 4
D. 2
Zadanie 5
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdej liczby rzeczywistej 𝑎 wyrażenie $(2a-3)^{2}-(2a+3)^{2}$ jest równe
A. $-24a$
B. $0$
C. $18$
D. $16a^{2}-24a$
Zadanie 6
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Zbiorem wszystkich rozwiązań nierówności $-2(x+3)\leq \frac{2-x}{3}$ jest przedział
A. $(-\infty ,-4]$
B. $(-\infty ,4]$
C. $(-4,\infty ]$
D. $(4,\infty ]$
Zadanie 7
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Jednym z rozwiązań równania $\sqrt{3}(x^{2}-2)(x+3)=0$ jest liczba
A. $3$
B. $2$
C. $\sqrt{3}$
D. $\sqrt{2}$
Zadanie 8
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Równanie $\frac{(x+1)(x-1)^{2}}{(x-1)(x+1)^{2}}=0$ w zbiorze liczb rzeczywistych
A. nie ma rozwiązania.
B. ma dokładnie jedno rozwiązanie: -1.
C. ma dokładnie jedno rozwiązanie: 1.
D. ma dokładnie dwa rozwiązania: -1 oraz 1.
Zadanie 9
Matematyka PP 2023 (0-1 pkt.)
Rozwiąż równanie
$3x^{3}-2x^{2}-12x+8=0$
Zapisz obliczenia.
Rozwiązanie:
[katex]x_{1}=-2;[/katex]
[katex]x_{2}=\frac{2}{3};[/katex]
[katex]x_{3}=2[/katex]
Rozwiązanie wideo:
Zadanie 10
Matematyka PP 2023 (0-1 pkt.)
Na rysunku przedstawiono interpretację geometryczną w kartezjańskim układzie współrzędnych (𝑥, 𝑦) jednego z niżej zapisanych układów równań A–D.
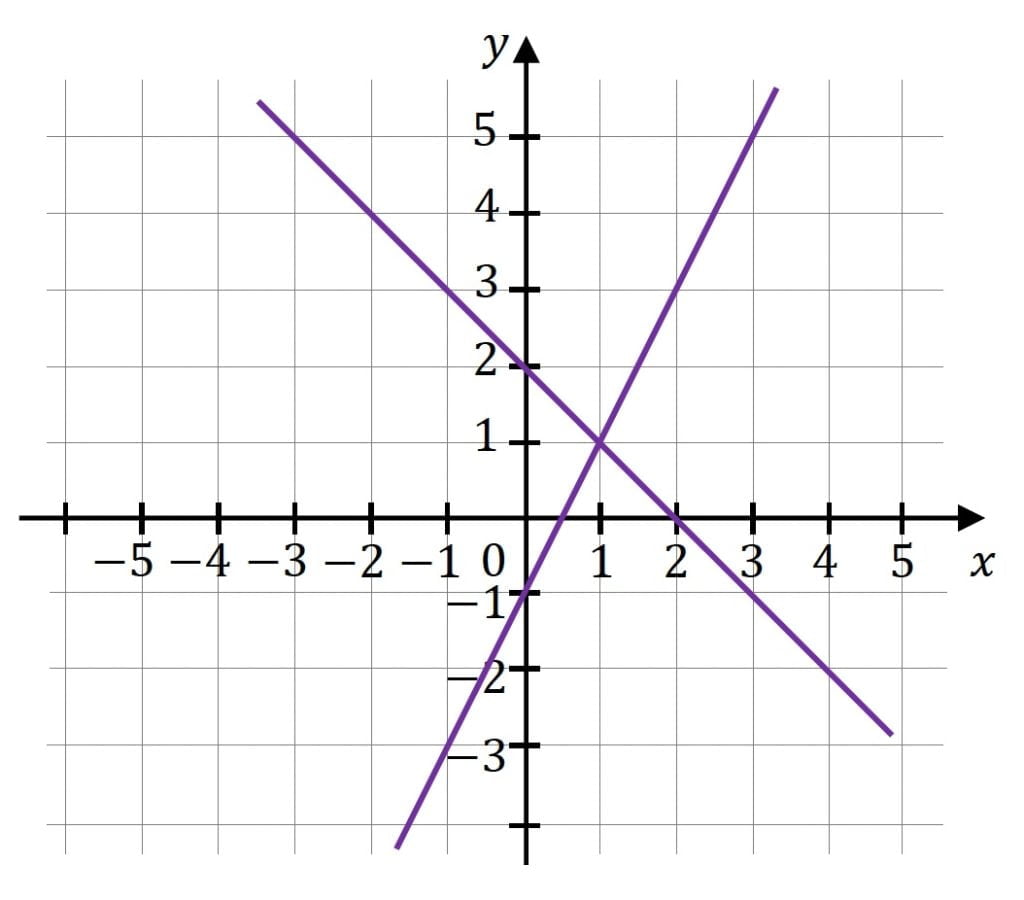
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Układem równań, którego interpretację geometryczną przedstawiono na rysunku, jest
A. $\begin{cases}
y=-x+2\\
y=-2x+1
\end{cases}
$
B. $\begin{cases}
y=x-2\\
y=-2x-1
\end{cases}
$
C. $\begin{cases}
y=x-2\\
y=2x+1
\end{cases}$
D. $\begin{cases}
y=-x+2\\
y=2x-1
\end{cases}
$
Zadanie 11
Matematyka PP 2023 (0-2 pkt.)
Dany jest prostokąt o bokach długości 𝑎 i 𝑏, gdzie 𝑎 > 𝑏. Obwód tego prostokąta jest równy 30. Jeden z boków prostokąta jest o 5 krótszy od drugiego.
Uzupełnij zdanie. Wybierz dwie właściwe odpowiedzi spośród oznaczonych literami A–F i wpisz te litery w wykropkowanych miejscach.
Zależności między długościami boków tego prostokąta zapisano w układach równań oznaczonych literami: ……… oraz ……… .
A. $\begin{cases}
2ab=30\\
a-b=5
\end{cases}$
B. $\begin{cases}
2a+b=30\\
a=5b
\end{cases}$
C. $\begin{cases}
2(a+b)=30\\
b=a-5
\end{cases}$
D. $\begin{cases}
2a+2b=30\\
b=5a
\end{cases}
$
E. $\begin{cases}
2a+2b=30\\
a-b=5
\end{cases}
$
F. $\begin{cases}
a+b=30\\
a=b+5
\end{cases}
$
Zadanie 12
Matematyka PP 2023 (0-3 pkt.)
W kartezjańskim układzie współrzędnych (𝑥, 𝑦) narysowano wykres funkcji 𝑦 = 𝑓(𝑥) (zobacz rysunek).
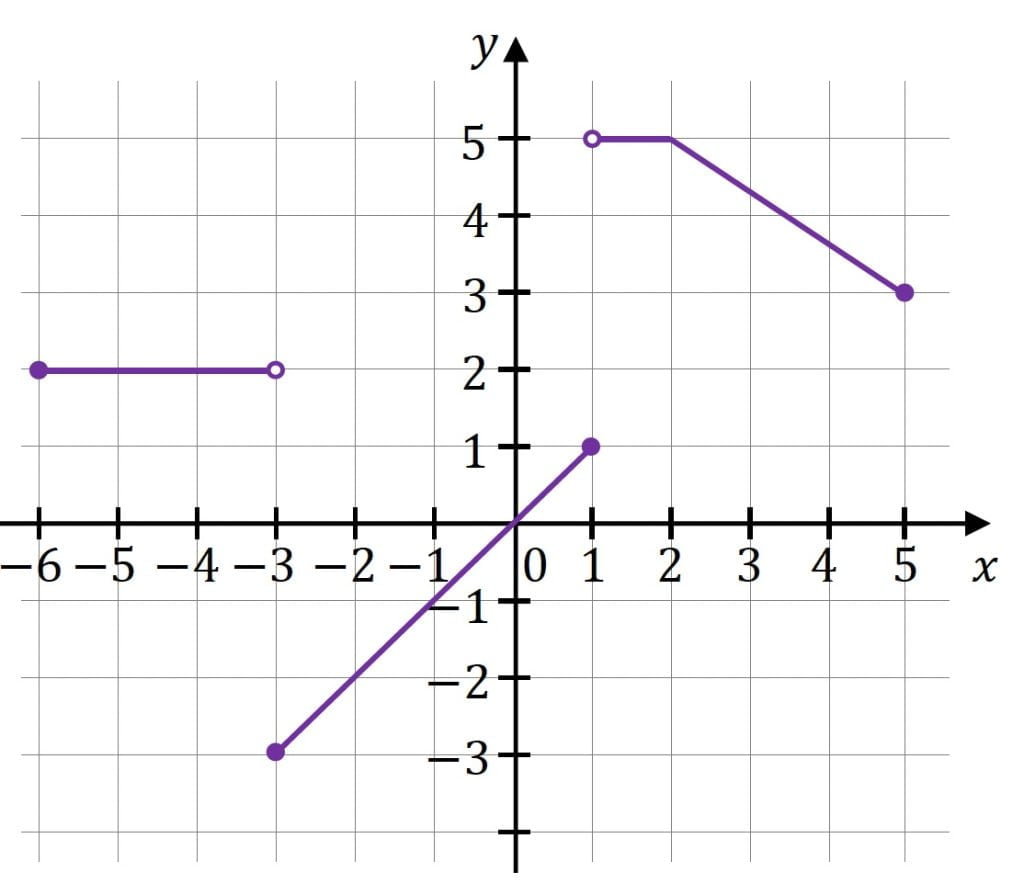
Zadanie 12.1
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dziedziną funkcji 𝑓 jest zbiór
A. [-6, 5]
B. (-6, 5)
C. (-3, 5]
D. [-3, 5]
Zadanie 12.2
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Największa wartość funkcji 𝑓 w przedziale [−4, 1] jest równa
A. 0
B. 1
C. 2
D. 5
Zadanie 12.2
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Funkcja 𝑓 jest malejąca w zbiorze
A. [-6, -3)
B. [-3, 1]
C. (1, 2]
D. [2, 5]
Zadanie 13
Matematyka PP 2023 (0-1 pkt.)
Funkcja liniowa 𝑓 jest określona wzorem 𝑓(𝑥) = 𝑎𝑥 + 𝑏, gdzie 𝑎 i 𝑏 są pewnymi liczbami rzeczywistymi. Na rysunku obok przedstawiono fragment wykresu funkcji 𝑓 w kartezjańskim układzie współrzędnych (𝑥, 𝑦).
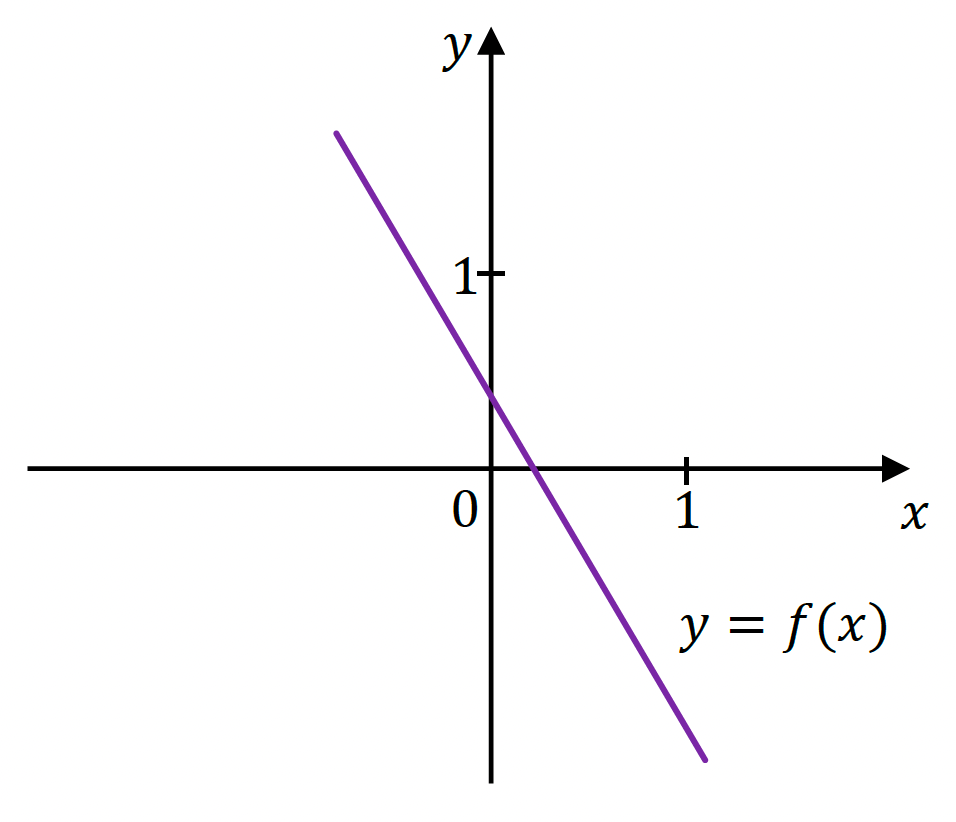
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 𝑎 oraz liczba 𝑏 we wzorze funkcji 𝑓 spełniają warunki:
A. 𝑎 > 0 i 𝑏 > 0.
B. 𝑎 > 0 i 𝑏 < 0.
C. 𝑎 < 0 i 𝑏 > 0.
D. 𝑎 < 0 i 𝑏 < 0.
Zadanie 14
Matematyka PP 2023 (0-1 pkt.)
Jednym z miejsc zerowych funkcji kwadratowej 𝑓 jest liczba (−5). Pierwsza współrzędna wierzchołka paraboli, będącej wykresem funkcji 𝑓, jest równa 3.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Drugim miejscem zerowym funkcji 𝑓 jest liczba
A. 11
B. 1
C. (-1)
D. (-13)
Zadanie 15
Matematyka PP 2023 (0-1 pkt.)
Ciąg $a_{n}$ określony wzorem $a_{n}=2^{n}\cdot (n+1)$ dla każdej liczby naturalnej $n\geq 1$.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wyraz $a_{4}$ jest równy
A. 64
B. 40
C. 48
D. 80
Zadanie 16
Matematyka PP 2023 (0-1 pkt.)
Trzywyrazowy ciąg (27, 9, 𝑎 − 1) jest geometryczny.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Liczba 𝑎 jest równa
A. 3
B. 0
C. 4
D. 2
Zadanie 17
Matematyka PP 2023 (0-2 pkt.)
Pan Stanisław spłacił pożyczkę w wysokości 8910 zł w osiemnastu ratach. Każda kolejna rata była mniejsza od poprzedniej o 30 zł.
Oblicz kwotę pierwszej raty. Zapisz obliczenia.
Zadanie 18
Matematyka PP 2023 (0-1 pkt.)
W kartezjańskim układzie współrzędnych (𝑥, 𝑦) zaznaczono kąt 𝛼 o wierzchołku w punkcie 𝑂 = (0, 0). Jedno z ramion tego kąta pokrywa się z dodatnią półosią 𝑂𝑥, a drugie przechodzi przez punkt 𝑃 = (−3, 1) (zobacz rysunek).
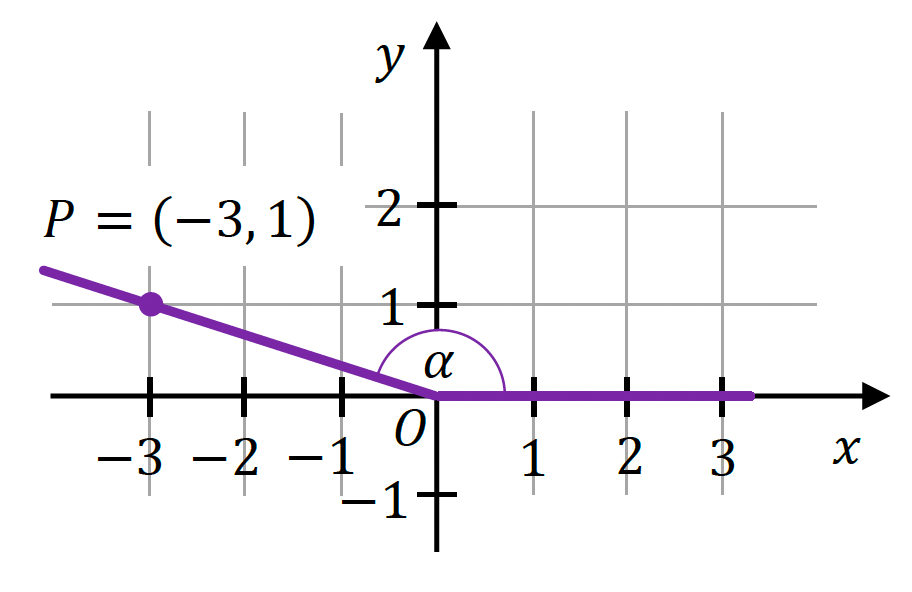
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Tangens kąta 𝛼 jest równy
A. $\frac{1}{\sqrt{10}}$
B. $(-\frac{3}{\sqrt{10}})$
C. $(-\frac{3}{1})$
D. $(-\frac{1}{3})$
Zadanie 19
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Dla każdego kąta ostrego $\alpha$ wyrażenie $\sin ^{4}\alpha +\sin ^{2}\alpha\cdot \cos ^{2}\alpha$ jest równe
A. $\sin ^{2}\alpha$
B. $\sin ^{6}\alpha\cdot \cos ^{2}\alpha$
C. $\sin ^{4}\alpha+1$
D. $\sin ^{2}\alpha\cdot (\sin\alpha+\cos\alpha)\cdot(\sin\alpha-\cos\alpha)$
Zadanie 20
Matematyka PP 2023 (0-1 pkt.)
W rombie o boku długości $6\sqrt{2}$ kąt rozwarty ma miarę $150°$.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Iloczyn długości przekątnych tego rombu jest równy
A. $24$
B. $72$
C. $36$
D. $36\sqrt{2}$
Zadanie 21
Matematyka PP 2023 (0-1 pkt.)
Punkty 𝐴, 𝐵, 𝐶 leżą na okręgu o środku w punkcie 𝑂. Kąt 𝐴𝐶𝑂 ma miarę 70° (zobacz rysunek).
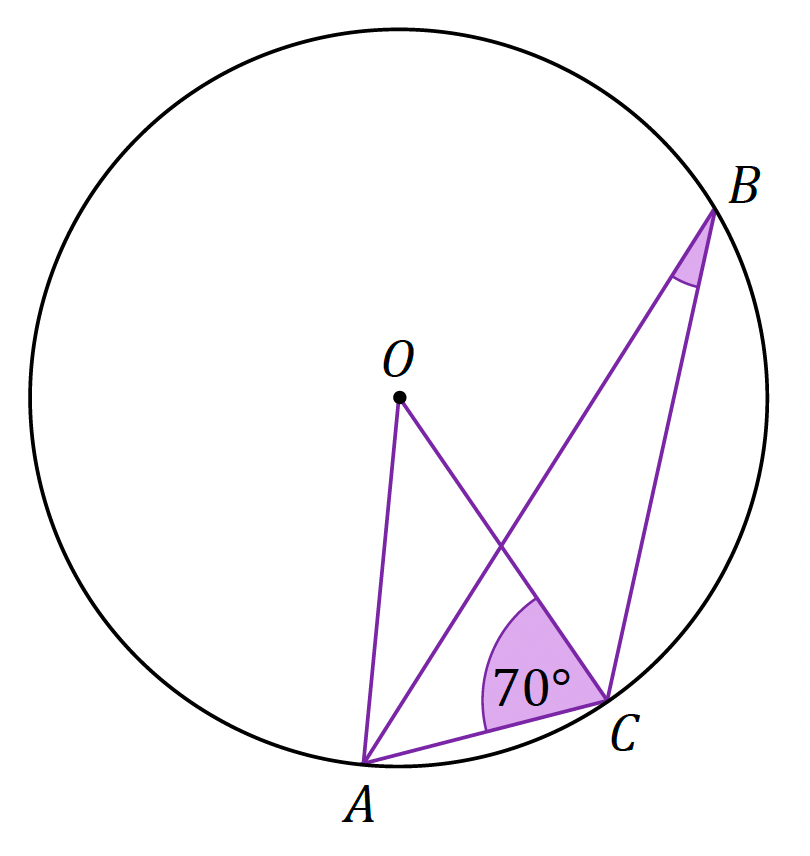
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Miara kąta ostrego 𝐴𝐵𝐶 jest równa
A. 10°
B. 20°
C. 35°
D. 40°
Zadanie 22
Matematyka PP 2023 (0-2 pkt.)
Trójkąty prostokątne $T_{1}$ i $T_{2}$ są podobne. Przyprostokątne trójkąta $T_{1}$ mają długości 5 i 12. Przeciwprostokątna trójkąta $T_{2}$ ma długość 26.
Oblicz pole trójkąta $T_{2}$. Zapisz obliczenia.
Zadanie 23
Matematyka PP 2023 (0-1 pkt.)
W kartezjańskim układzie współrzędnych (𝑥, 𝑦) dane są proste 𝑘 oraz 𝑙 o równaniach
$k: y=\frac{2}{3}x$
$l: y=-\frac{3}{2}x+13$
Dokończ zdanie. Wybierz odpowiedź A albo B oraz odpowiedź 1., 2. albo 3.
Proste 𝑘 oraz 𝑙

Zadanie 24
Matematyka PP 2023 (0-1 pkt.)
W kartezjańskim układzie współrzędnych (𝑥, 𝑦) dana jest prosta 𝑘 o równaniu
$y=-\frac{1}{3}x+2$
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Prosta o równaniu $y=ax+b$ jest równoległa do prostej 𝑘 i przechodzi przez punkt 𝑃 = (3, 5), gdy
A. $a=3$ i $b=4$.
B. $a=\frac{1}{3}$ i $b=4$.
C. $a=3$ i $b=-4$.
D. $a=-\frac{1}{3}$ i $b=6$.
Zadanie 25
Matematyka PP 2023 (0-1 pkt.)
Dany jest graniastosłup prawidłowy czworokątny, w którym krawędź podstawy ma długość 15. Przekątna graniastosłupa jest nachylona do płaszczyzny podstawy pod kątem $\alpha$ takim, że $\cos \alpha =\frac{\sqrt{2}}{3}$.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Długość przekątnej tego graniastosłupa jest równa
A. $15\sqrt{2}$
B. $45$
C. $5\sqrt{2}$
D. $10$
Zadanie 26
Matematyka PP 2023 (0-4 pkt.)
Dany jest ostrosłup prawidłowy czworokątny. Wysokość ściany bocznej tego ostrosłupa jest nachylona do płaszczyzny podstawy pod kątem 30° i ma długość równą 6 (zobacz rysunek).
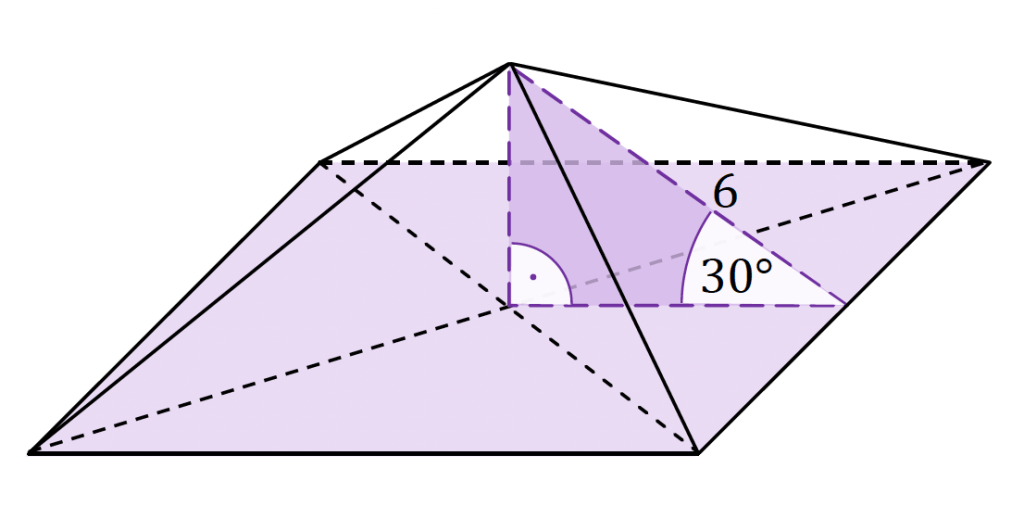
Oblicz objętość i pole powierzchni całkowitej tego ostrosłupa. Zapisz obliczenia.
Zadanie 27
Matematyka PP 2023 (0-1 pkt.)
W pewnym ostrosłupie prawidłowym stosunek liczby 𝑊 wszystkich wierzchołków do liczby 𝐾 wszystkich krawędzi jest równy $\frac{W}{K}=\frac{3}{5}$.
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Podstawą tego ostrosłupa jest
A. kwadrat.
B. pięciokąt foremny.
C. sześciokąt foremny.
D. siedmiokąt foremny.
Zadanie 28
Matematyka PP 2023 (0-1 pkt.)
Dokończ zdanie. Wybierz właściwą odpowiedź spośród podanych.
Wszystkich liczb naturalnych pięciocyfrowych, w których zapisie dziesiętnym występują tylko cyfry 0, 5, 7 (np. 57 075, 55 555), jest
A. $5^{3}$
B. $2\cdot 4^{3}$
C. $2\cdot 3^{4}$
D. $3^{5}$
Zadanie 29
Matematyka PP 2023 (0-2 pkt.)
Na diagramie poniżej przedstawiono ceny pomidorów w szesnastu wybranych sklepach.
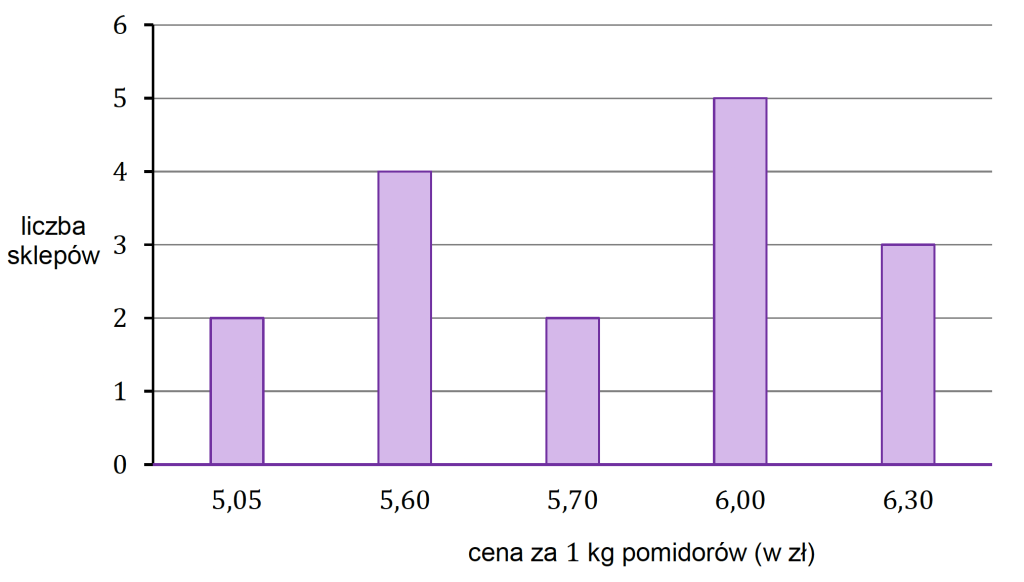
Uzupełnij tabelę. Wpisz w każdą pustą komórkę tabeli właściwą odpowiedź, wybraną spośród oznaczonych literami A–E.

A. 5,80 zł
B. 5,73 zł
C. 5,85 zł
D. 6,00 zł
E. 5,70 zł
Zadanie 30
Matematyka PP 2023 (0-2 pkt.)
Ze zbioru ośmiu liczb {2, 3, 4, 5, 6, 7, 8, 9} losujemy ze zwracaniem kolejno dwa razy po jednej liczbie.
Oblicz prawdopodobieństwo zdarzenia 𝑨 polegającego na tym, że iloczyn wylosowanych liczb jest podzielny przez 𝟏𝟓. Zapisz obliczenia.
Zadanie 31
Matematyka PP 2023 (0-3 pkt.)
Właściciel pewnej apteki przeanalizował dane dotyczące liczby obsługiwanych klientów z 30 kolejnych dni. Przyjmijmy, że liczbę 𝐿 obsługiwanych klientów $n$-tego dnia opisuje funkcja
$L(n)=-n^{2}+22n+279$
gdzie $n$ jest liczbą naturalną spełniającą warunki $n\geq 1$ i $n\leq 30$.
Zadanie 31.1
Matematyka PP 2023 (0-1 pkt.)
Oceń prawdziwość poniższych stwierdzeń. Wybierz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli jest fałszywe.

Zadanie 31.2
Matematyka PP 2023 (0-2 pkt.)
Którego dnia analizowanego okresu w aptece obsłużono największą liczbę klientów? Oblicz liczbę klientów obsłużonych tego dnia. Zapisz obliczenia.
Odpowiedź:
Zadanie 31.1: F P
Zadanie 31.2: 11 dnia obsłużono największą liczbę klientów – było to 400 osób
